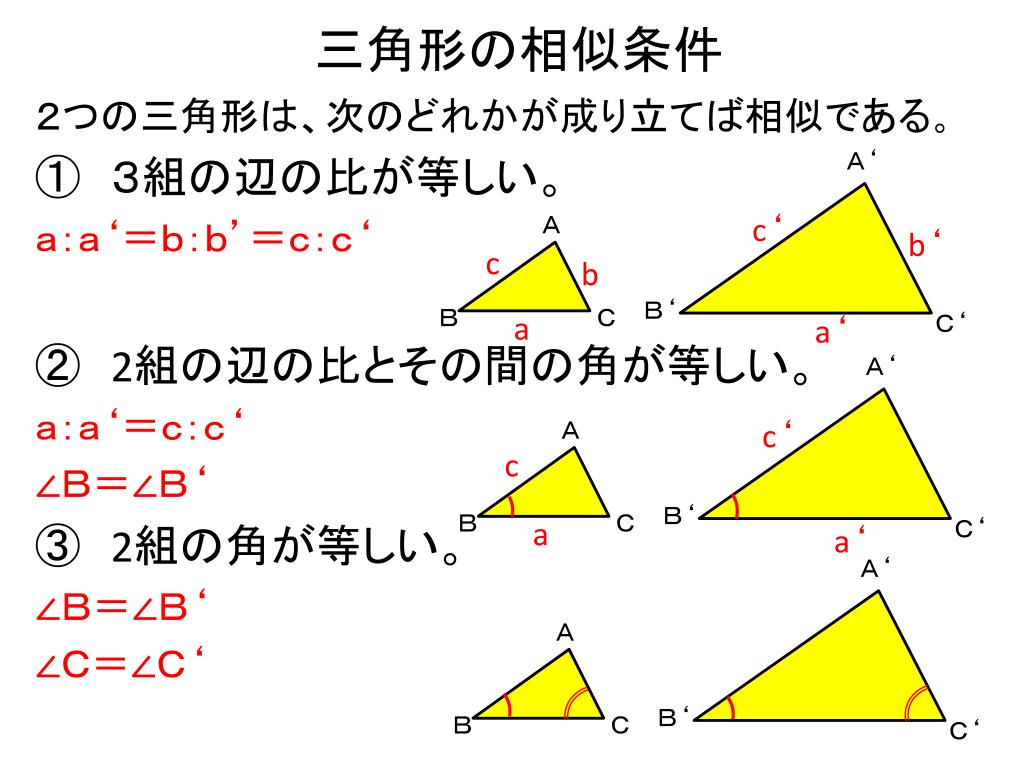
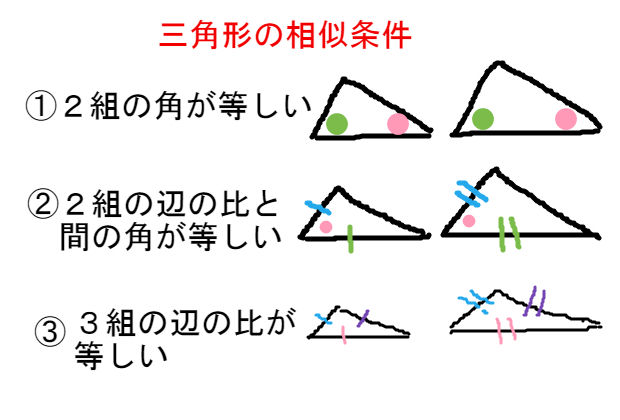
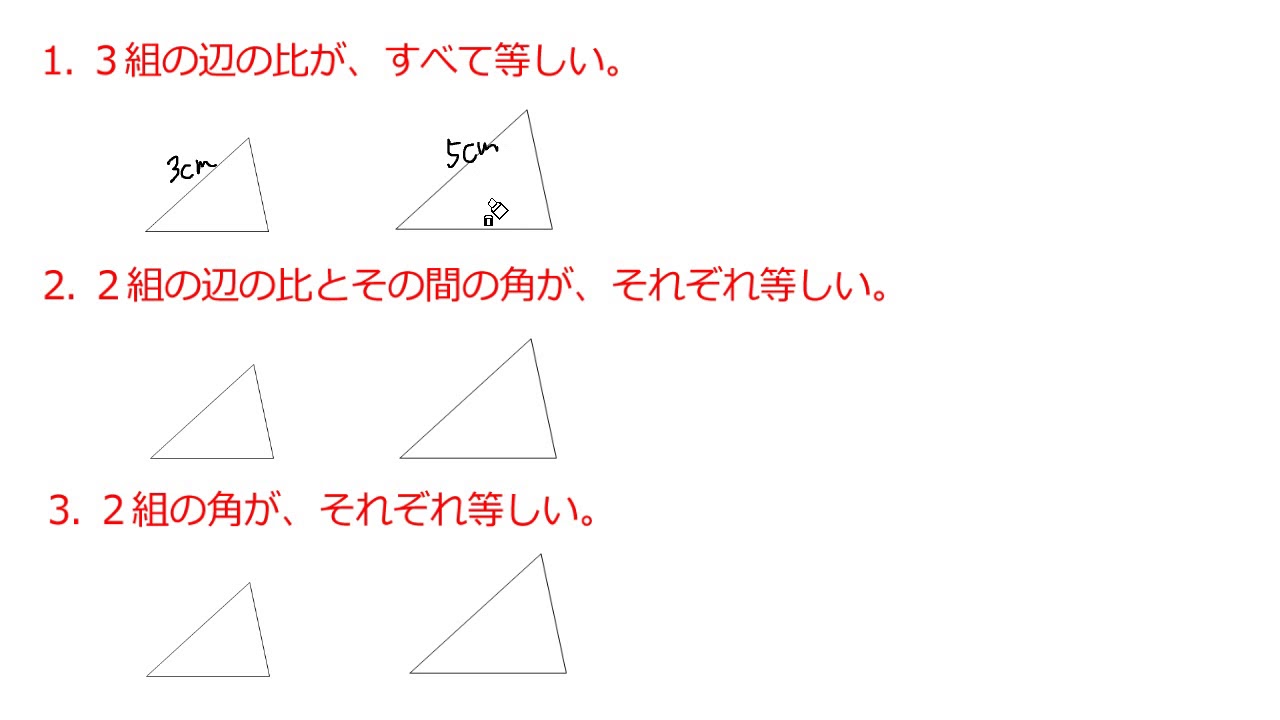
三角形の相似条件 中3数学 証明問題で最も出題されるのがこの相似の証明です。 使う相似条件は99%「2組の角がそれぞれ等しい」と言って過言ではありません。 とにかく等しい角を2つ見つけることを心がけてください。中3_三角形の相似_円錐の体積比(日本語版) Watch later Share Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendationsつまり,三角形の相似条件は, 3辺 がそれぞれ等しい→ 3組の辺の比 がすべて等しい 2辺 とその間の角がそれぞれ等しい→ 2組の辺の比 とその間の角がそれぞれ等しい 1辺 とその両端の角がそれぞれ等しい→2組の角がそれぞれ等しい となります。 3の

数学 中3 48 相似の証明チャレンジ Lv 3 Youtube
三角形 の 相似
三角形 の 相似-三角形の相似条件 とは、2つの三角形が相似であることを示すための条件です。 以下の3つの相似条件のうち、どれかが成り立つ場合、その三角形は相似であるといえます。 3組の辺の比がすべて等しい。 2組の辺の比が等しく、その間の角が等しい。 2組の角がそれぞれ等しい。 このページの続きでは、三角形の図を見ながら、これらの相似条件を確認していき q1 三角形の相似条件として、正しくないものを選びましょう。 3組の辺の比がそれぞれ等しい。 2組の辺の長さとその間の角



三角形の相似条件の解説 図形の性質
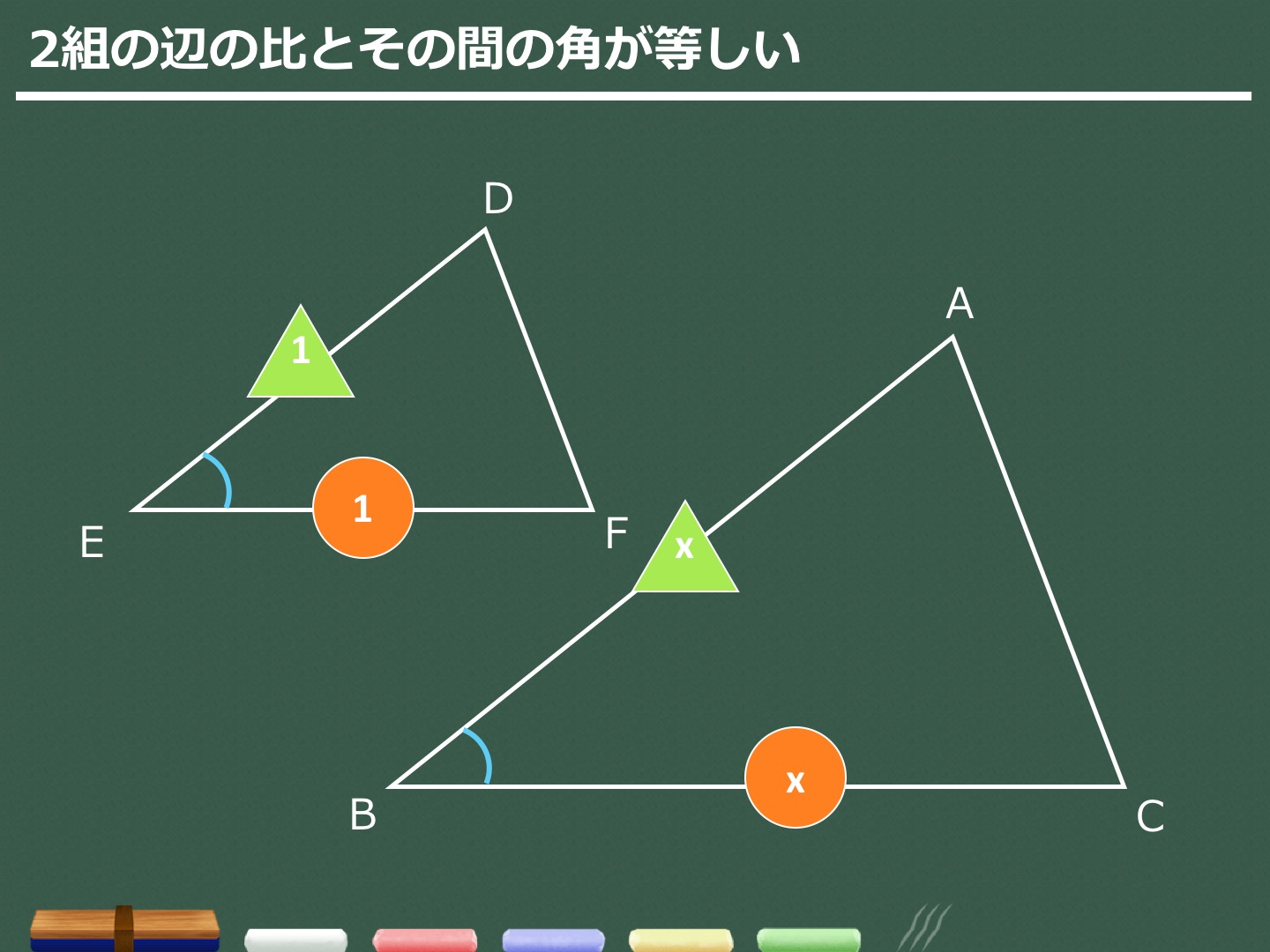
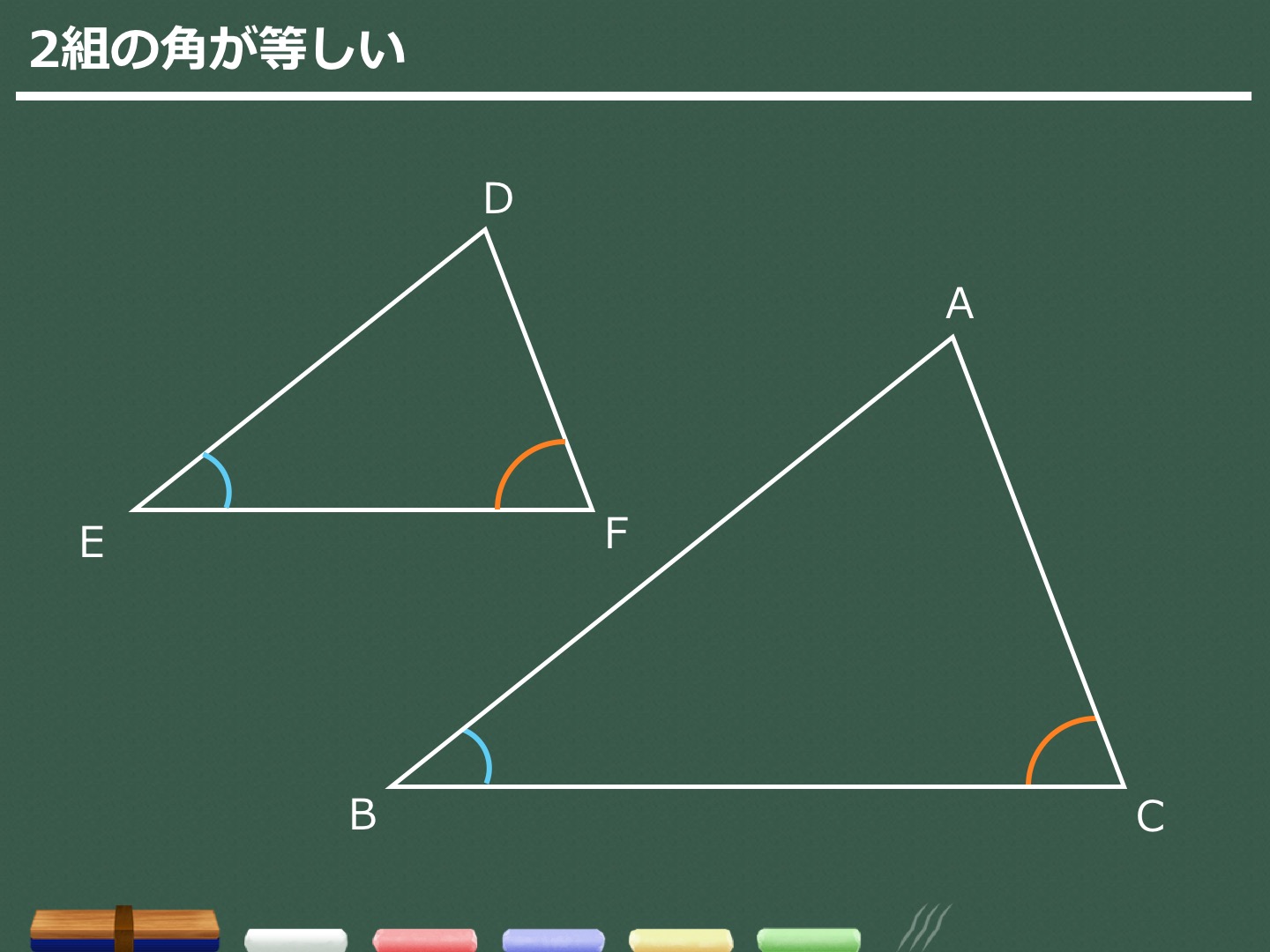
今天小编就为大家精心整理了一篇有关学习计划的相关内容,以供大家阅读,更多信息请关注学习方法网! 相似三角形的定义 对应角相等、对应边成比例的两个三角形叫做相似三角形。 如果三边分别对相似三角形を英語に訳すと。英訳。similar triangles 80万項目以上収録、例文・コロケーションが豊富な無料英和和英辞典。三角形の相似条件 2つの三角形は,次の各場合に相似である。 (ア)3組の辺の比がすべて等しいとき (イ)2組の辺の比とその間の角がそれぞれ等しいとき (ウ)2組の角がそれぞれ等しいとき 内容を式で表すと (ア)a:d =b:e =c:f (イ)a:d =b:e ,∠C =∠F
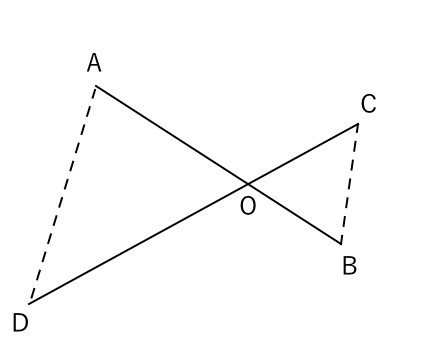
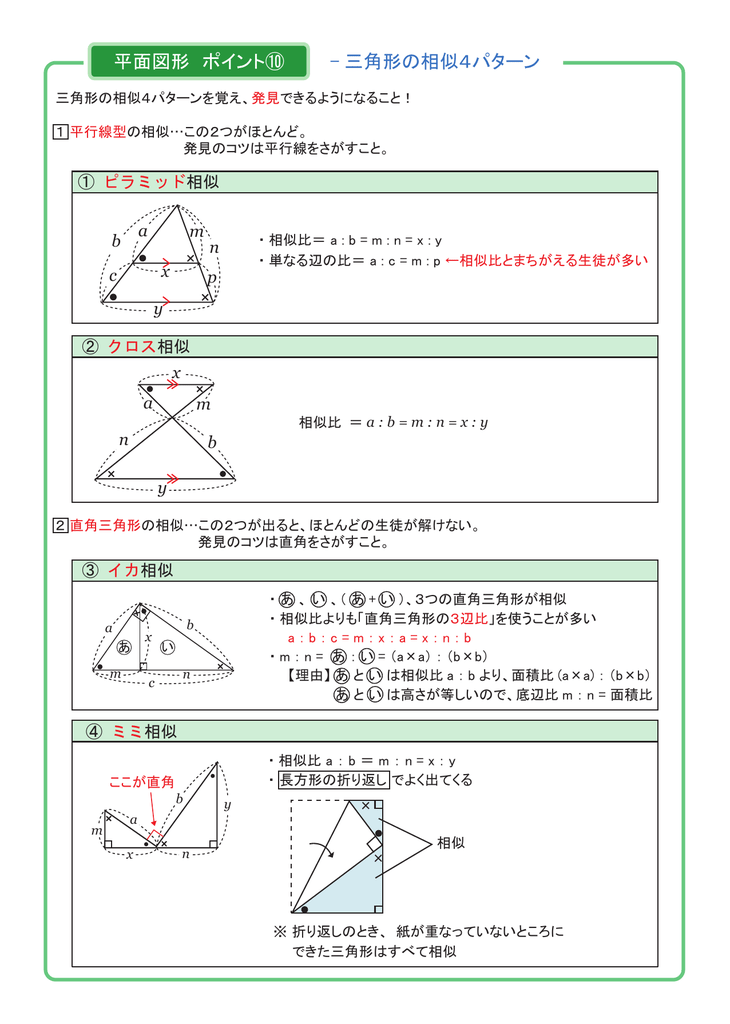
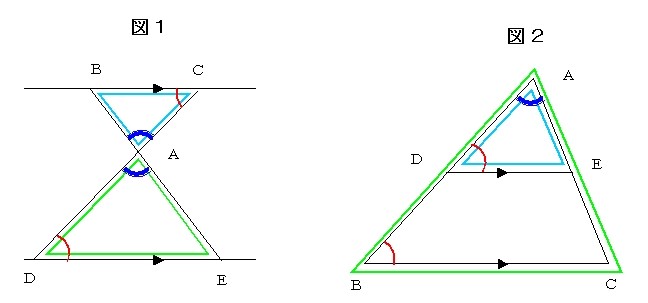
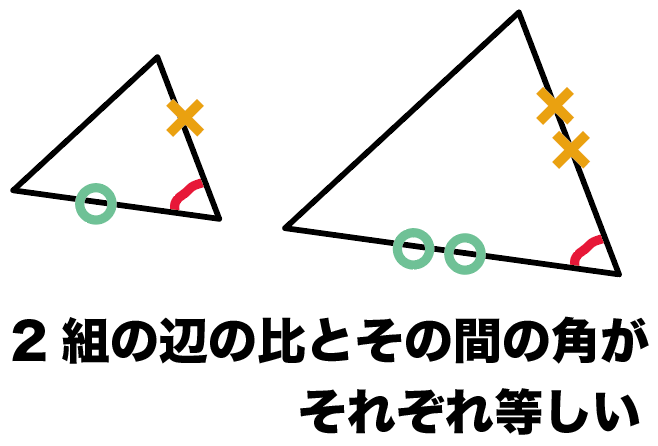
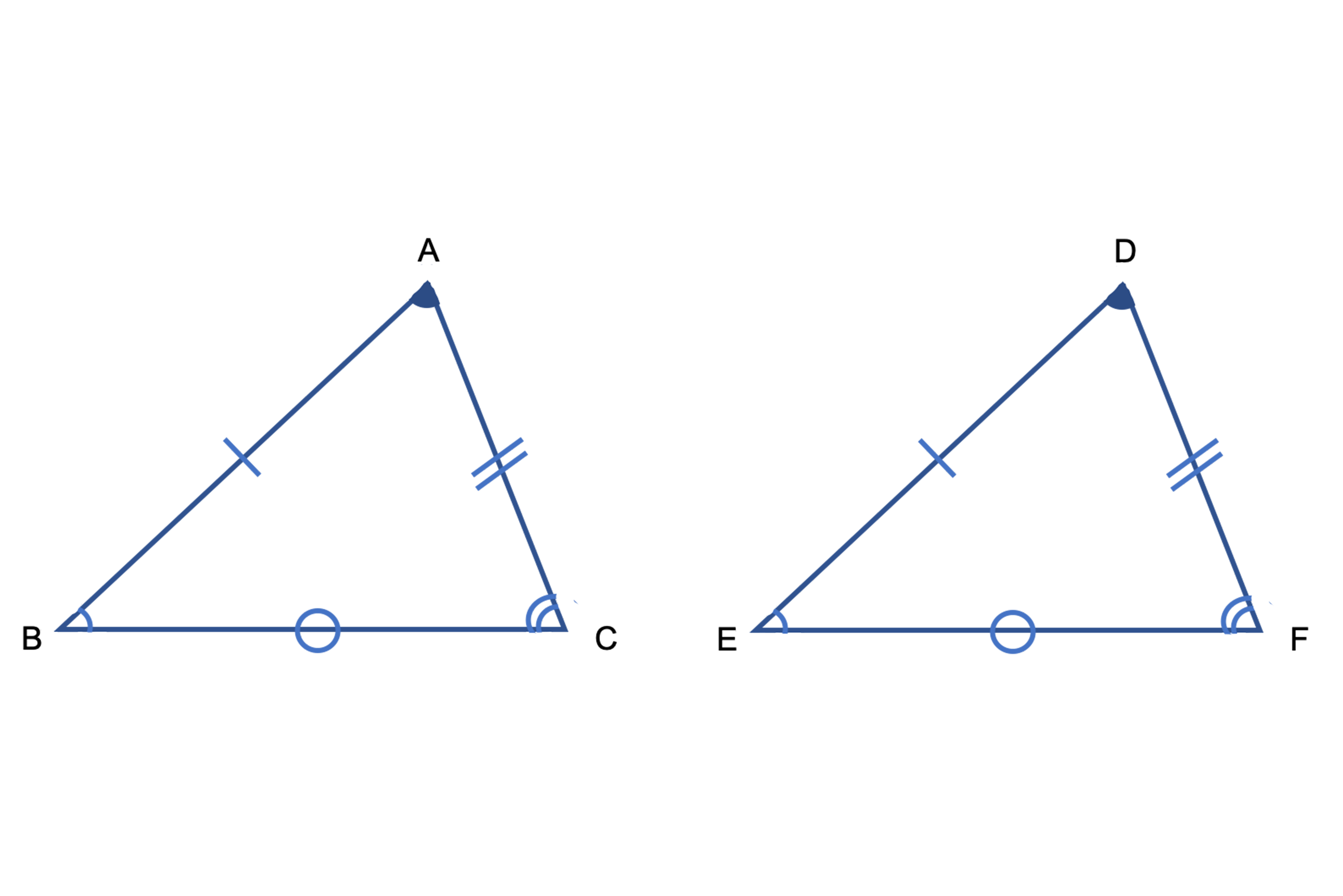
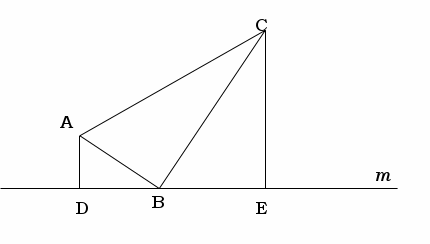
三角形(ピラミッド型)の相似 「三角形が重なる形(ピラミッド型)+平行→相似」 という発想が大事です。 「二本の線が平行」→同位角が同じ→2角が同じなので相似の三角形 ~~~~~~~~~~~~~~~~~~~~~~~~~ 相似のテクニック 1)2組の角度が同じならその三角形どうしは相似になるSimilar transformation (相似形の変身) ワークシート okyota Fold the rectangle (長方形の折り返し 相似) ワークシート okyota Fold the rectangle (長方形の折り返し 相似)minor change三角形の相似条件 三角形の相似条件 2つの三角形は次の各場合に相似である。 1 3組の辺の比が、すべて等しいとき 2 2組の辺の比とその間の角が、それぞれ等しいとき 3 2組の角が、それぞれ等しい
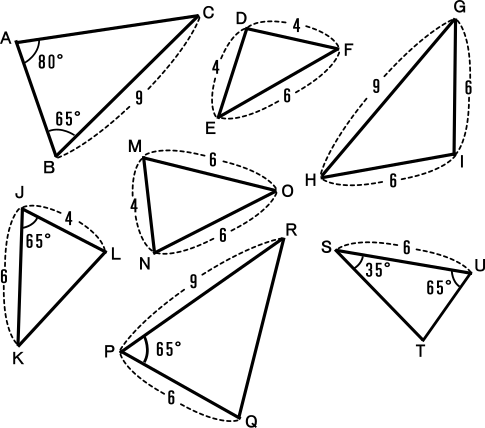
複素平面での三角形の相似 点$\rm{P(\it{z}_1\rm), Q(\it{z}\rm _2\rm), R(\it z \rm _3), P'(\it w \rm_1), Q'(\it w \rm _2), R'(\it w \rm _3)}$に対し $$\triangle{\rm{PQR}}\text{と} \triangle{\rm{P'Q'R'}} \text{は同じ向きに相似} \Leftrightarrow \frac{z_3z_1}{z_2z_1}=\frac{w_3w_1}{w_2w_1}$$ 三角形相似的判定条件 两角对应相等,两个三角形相似;两边对应成比例且夹角相等,两个三角形相似;三边对应成比例,两个三角形相似;三边对应平行,两个三角形相似;斜边与直角边对应成比例,两个直角三角形相似;全等三角形相似。 1如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。 (简叙为:两角对应相等,两个− 102 − 高校講座・学習メモ 三角形の相似 q: 次の三角形はどれとどれが相似でしょう? b 65°65°



高校入試対策数学 折り返し図形と相似の融合問題 中学生勉強サイトあかね先生



相似な図形 証明に慣れよう 苦手な数学を簡単に
゚ 三角形の相似曵件。 ゜ 平行線および平行平面に関する線分の比についての性質。 ゞ 三角形および平行四辺形の性質。 (3) 縮図や立体図形の相似を通して,相似についての理解を济める。 ゚ 簡単な立体図形の相似,および相似形の相似比と面積比ン体動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru受力分析中的"相似三角形"方法 这里主要讲的是"三力平衡"问题。 分析平衡问题,一般采用的是力的合成或者分解方法,分解又以正交分解为"正统"。 后来,我又跟小伙伴们分享了"拉密定理",而拉密定理




数学 中3 48 相似の証明チャレンジ Lv 3 Youtube



Studydoctor相似な三角形の辺の比 中3数学 Studydoctor
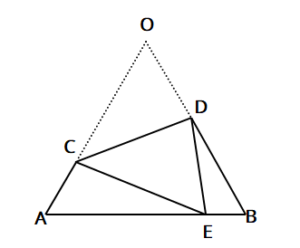
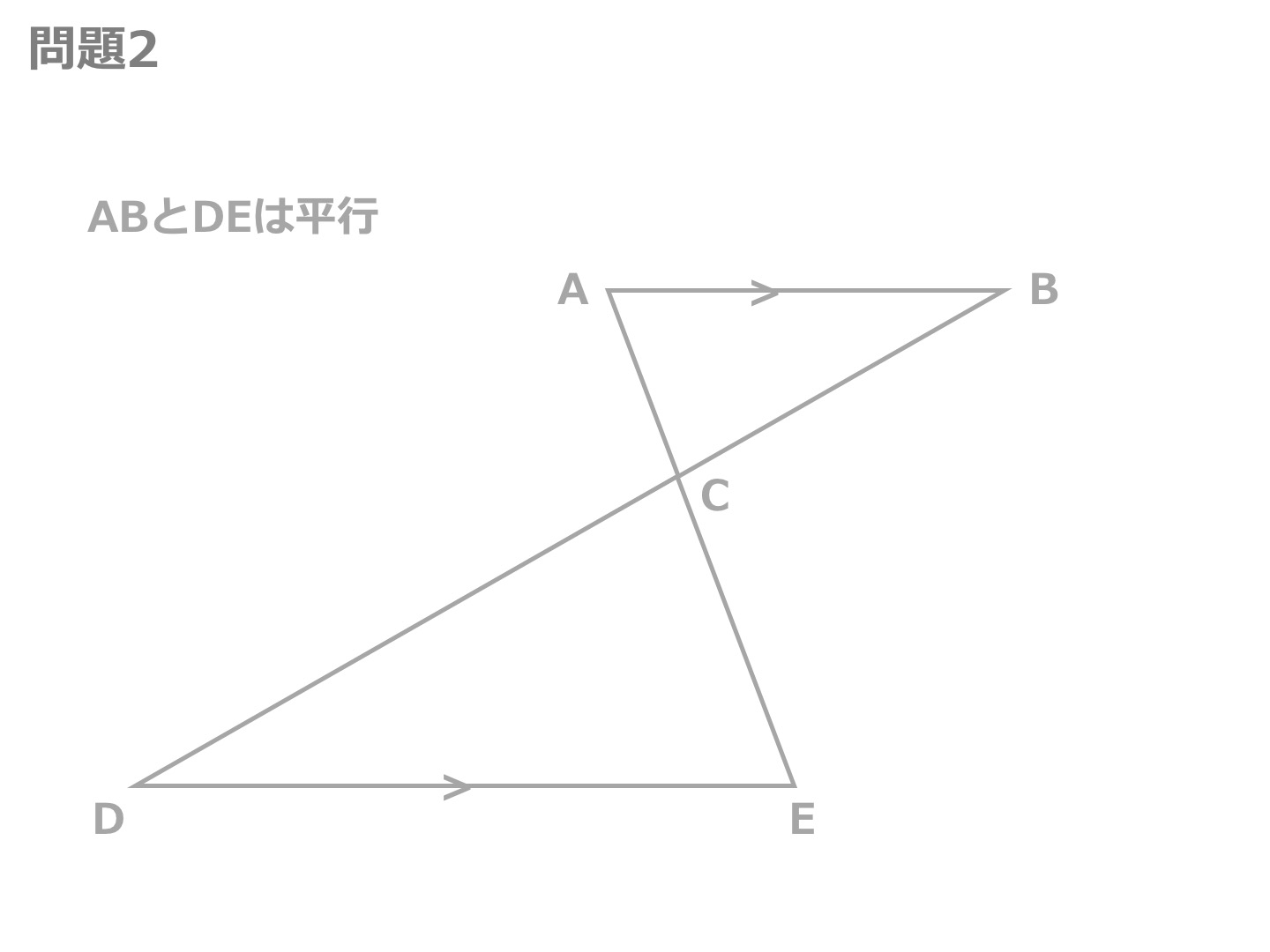
相似三角形 如果两个三角形只是大小不同(也可能要把其中一个翻转或旋转),那么它们便是 相似 的。 这些三角形都是相似的: (相等的角用同个数的弧线标记) 它们有些是大小不同的,也有些是旋转或翻转了的。 两个相似三角形: 所有的对应角 (2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。 相似三角形 定义 三角分别相等,三边成比例的两个三角形叫做相似三角形。 性质 1相似三角形对应角相等,对应边成比例。この条件で、なぜ2つの三角形が「相似」であることが言えるのか、その理由を説明しなさい。 相似③三角形の相似条件d 学 年 3年 学習日: 月 日( ) 中学校数学 3b5-3d 中学校数学・ワークブック 年 組 氏名



相似な図形 相似条件の練習問題 苦手な数学を簡単に



相似比とは 1分でわかる意味 面積比 四角形と三角形の問題
这两个相似三角形的边比例是 2:1(一个三角形的边是另一个的两个倍): 那么它们的面积呢? 如果我们多画三条线,答案就浅而易见: 我们可以看到可以有四个小三角形放在大三角形里。 因此,如果长度是两倍,面积便是四倍 面积的比是 4:1 4:1 也可以三角形の相似条件 3組の辺の比 がそれぞれ等しい 2組の辺の比 と その間の角 がそれぞれ等しい 2組の角 がそれぞれ等しい 合同条件と似ているのがわかるかと思います。 1番目と2番目は「辺」が「辺の比」になり、3番目は「辺の長さに関する条件」がなくなったものです。 ではこの三角形の相似条件をどのように使うのか、実際に問題を解きながら見ていき 相似な三角形を使った練習問題 下の図の ABCで、∠BACの二等分線と辺BCとの交点をDとし、線分ADの垂直二等分線と辺AB,ACとの交点をそれぞれE、Fとする。 EとD、FとDをそれぞれ結ぶ。 このとき、次の問いに答えなさい。 (1)∠EADと大きさが等しい角は∠FAD



中学3年数学練習問題 三角形の相似条件の問題




三角形の相似条件と基本的な証明 無料で使える中学学習プリント
三角形の相似条件 三角形の相似を証明するためには、「相似条件」というものを使います。 相似条件には、以下の \(3\) つがあります。 相似条件①3 組の辺の比がそれぞれ等しい \(3\) 辺の比がそれぞれ等しければ、相似と言えます。



三角形の相似の証明 2 ネット塾



三角形の相似条件の解説 図形の性質




三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



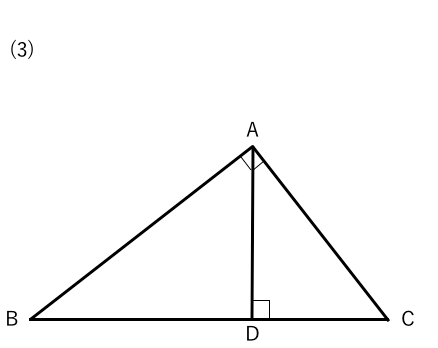
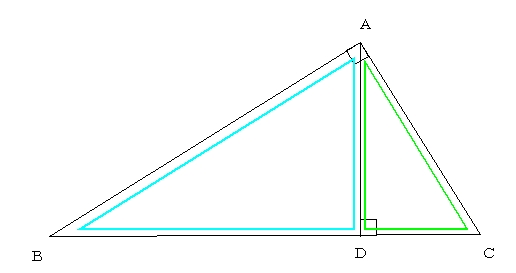
直角三角形の相似条件 具体例で学ぶ数学




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題




三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典



正三角形と相似 中学数学の無料オンライン学習サイトchu Su



中学数学 相似の証明 その2 中学数学の無料オンライン学習サイトchu Su



相似な図形 三角形の相似条件 相似比 勉強ナビゲーター



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス




三角形の相似条件



Ppt 相似条件と証明 Powerpoint Presentation Free Download Id



高校入試数学 相似な三角形の対策問題




Descubre Como Resolverlo En Qanda



平面図形 ポイント 三角形の相似4パターン



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス



三角形の相似 合同条件 中学数学 理科 寺子屋塾の復習サイト



相似の証明 2つの正三角形と共通な角 勉強ナビゲーター



相似 直角三角形
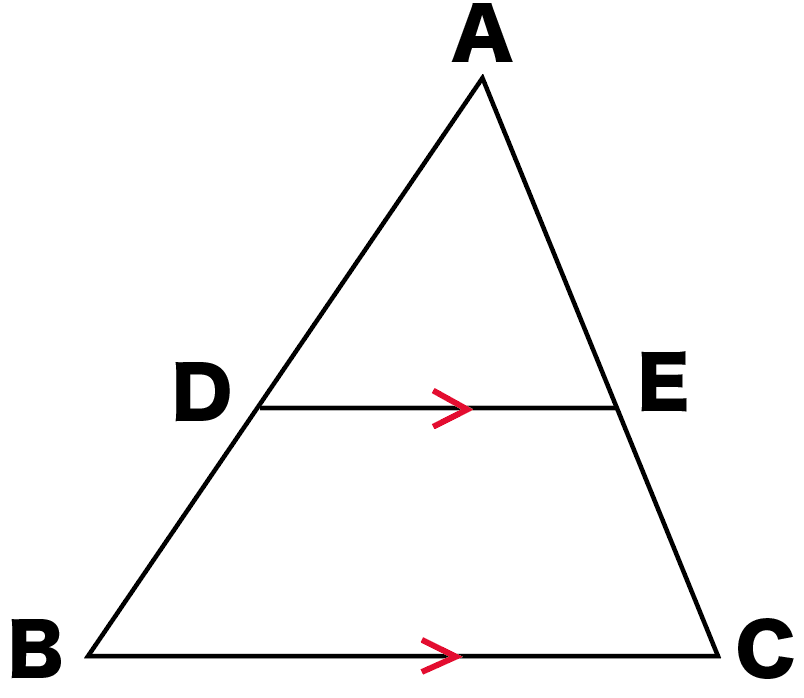



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく




相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学
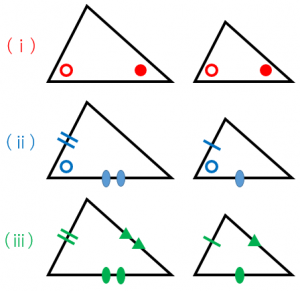



三角形の相似条件と有名な例題3問 具体例で学ぶ数学
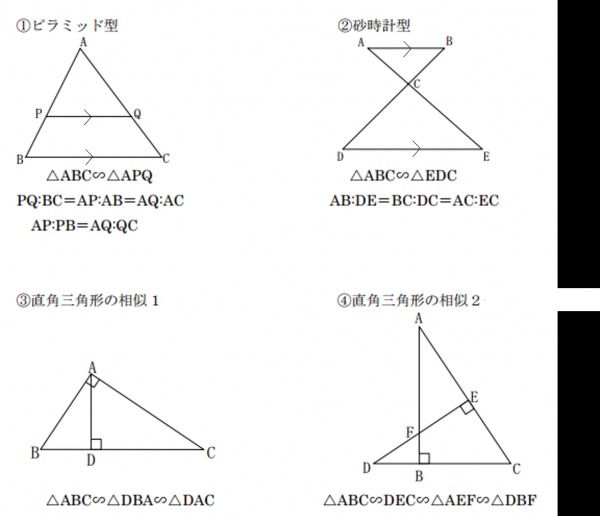



三角形の相似 合同条件 優技録



1
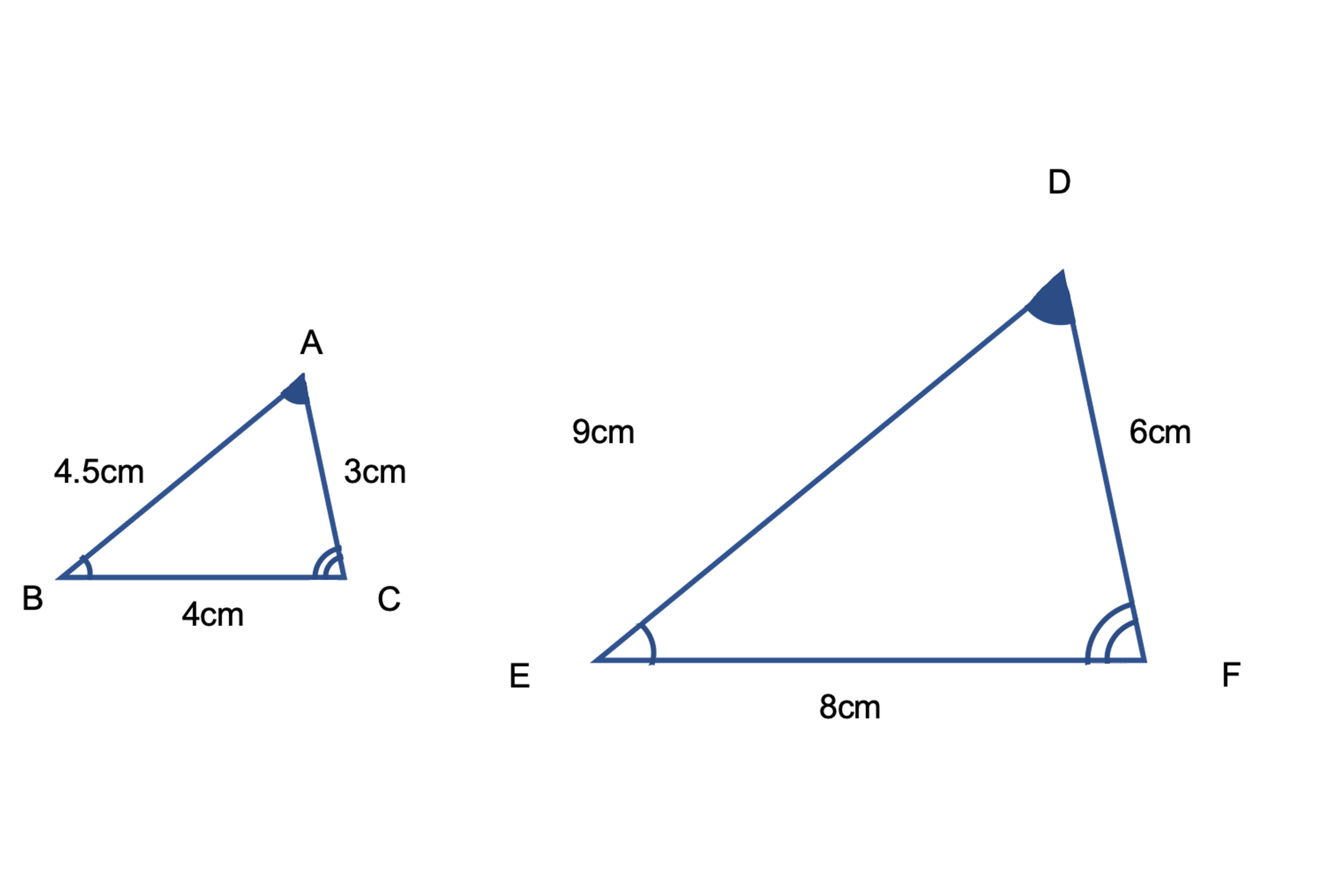



記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス




三角形の面積比と相似比 チーム エン




平面図形の苦手を解消 三角形の面積比 基本編



相似 直角三角形




三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題




三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




中3数学 相似 直角三角形と相似 Youtube




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく



Studydoctor正三角形と相似の証明 中3数学 Studydoctor




中3数学 三角形の相似条件2 2辺の比とその間の角 練習編 映像授業のtry It トライイット




三角形の相似条件 イ弋マ本ゼミナール




相似な三角形を見つける 修正 Youtube



合同とは 相似とは



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ
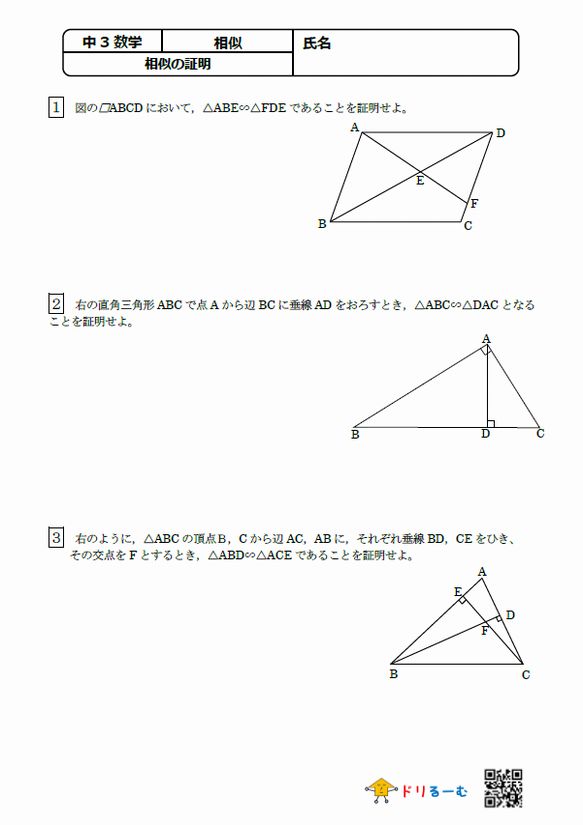



三角形の相似条件 ドリるーむ
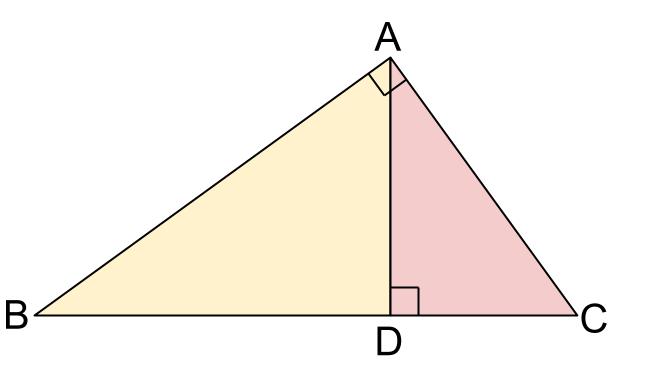



中学数学 直角三角形の相似 中学数学の無料オンライン学習サイトchu Su
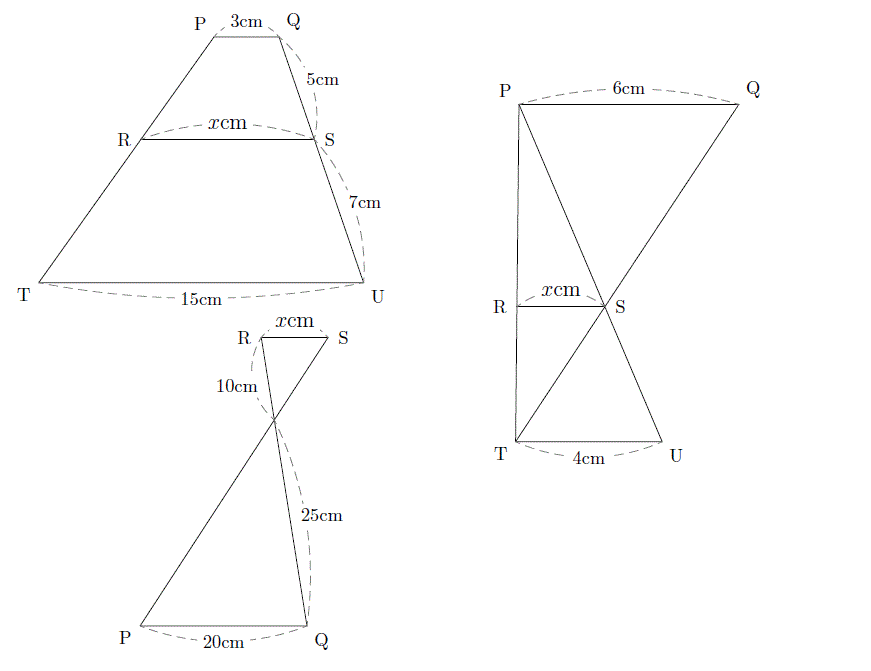



かみのドリル 相似



直角三角形の相似条件 具体例で学ぶ数学



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



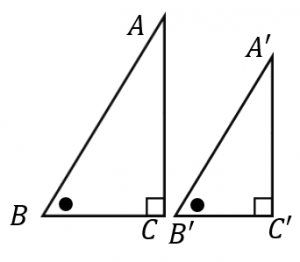
中学数学 相似の証明 その1 中学数学の無料オンライン学習サイトchu Su




中3数学 三角形の相似条件1 3辺の比 映像授業のtry It トライイット



6 1 2 Descubre Como Resolverlo En Qanda



2分でわかる 三角形の3つの相似条件 Qikeru 学びを楽しくわかりやすく




5章1節2 三角形の相似条件2 数学のすすめ




三角形の相似条件



記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス



中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ



三角形の相似条件的副本 Geogebra




相似な図形 補助線を引いて考える相似の問題 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ




数学 中3 44 三角形の相似条件 Youtube



3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ




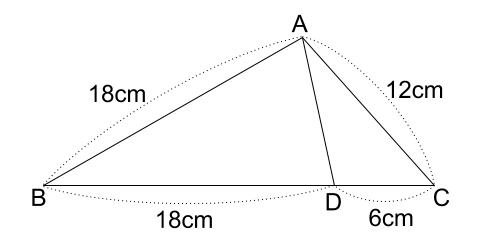
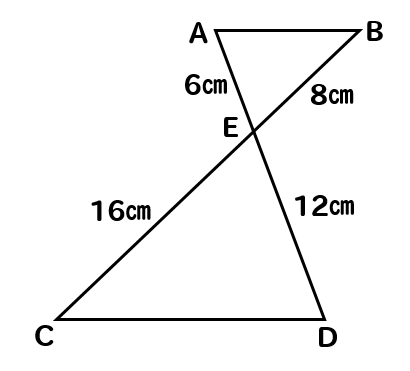
至急 この問題の相似な三角形と相似条件を教えてください 考え方が分かりません Clear



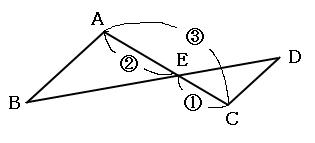
相似の証明2



相似な図形の問題の解き方を解説 相似は隠れたチョウチョとトンガリを探すべし




Descubre Como Resolverlo En Qanda
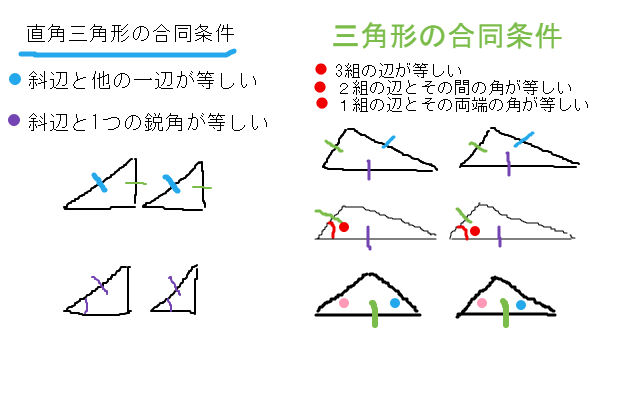



三角形 合同 相似条件 直角三角形の合同条件 中学数学 理科 寺子屋塾の復習サイト




三角形の相似条件と証明問題の解き方 数学fun




相似な図形 三角形の相似条件 中学数学 By となりがトトロ マナペディア
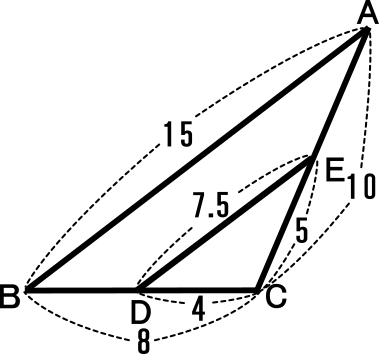



中学3年数学練習問題 三角形の相似条件と証明の問題



1
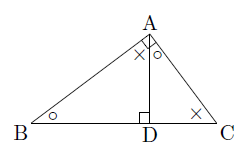



直角三角形と相似 まなびの学園




中3数学 相似比とは 例題編 映像授業のtry It トライイット



平面図形の基礎
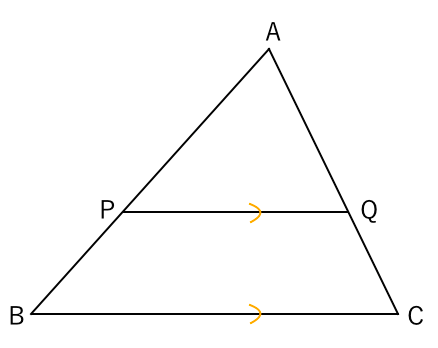



相似な図形 計算について覚えること 苦手な数学を簡単に
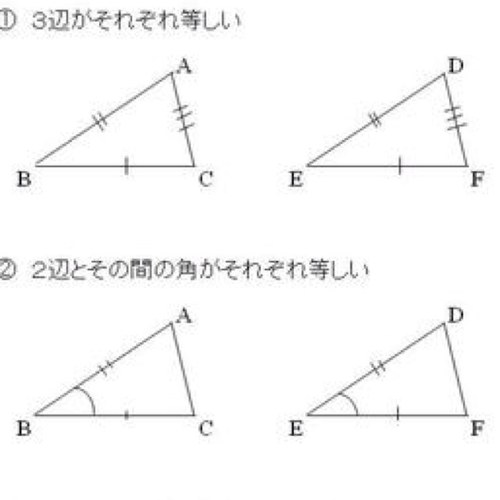



三角形の相似条件bot Triangle Bot Twitter




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学



三角形の相似条件




Math 相似 直角三角形 正三角形と相似 働きアリ




相似の問題は2通りの解き方があります セルモ大蔵 世田谷 の塾長ブログ



3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ



3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ




三角形の相似条件



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス
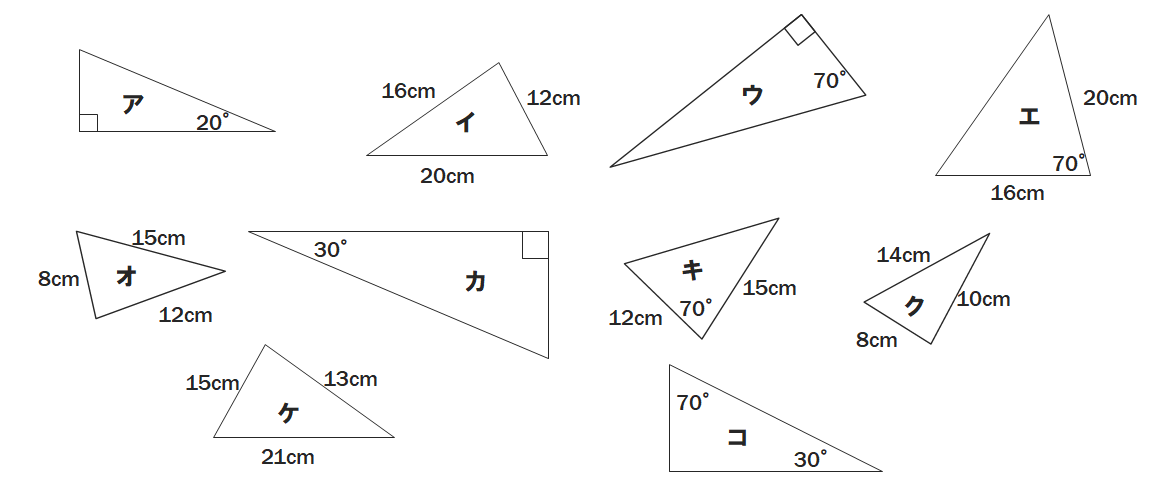



中3数学 相似な図形の線分比の定期テスト対策問題 Examee



相似 平行 三角形と線分の比 勉強ナビゲーター
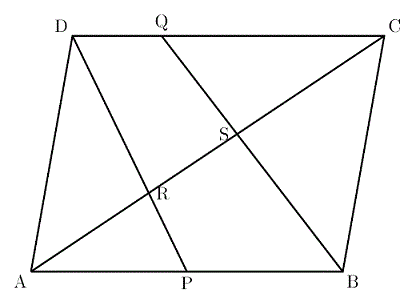



かみのドリル 三角形の相似のドリル 中受




この3問がどうしても わかりません 回答お願いいたします もしよければ途中経過も Clear
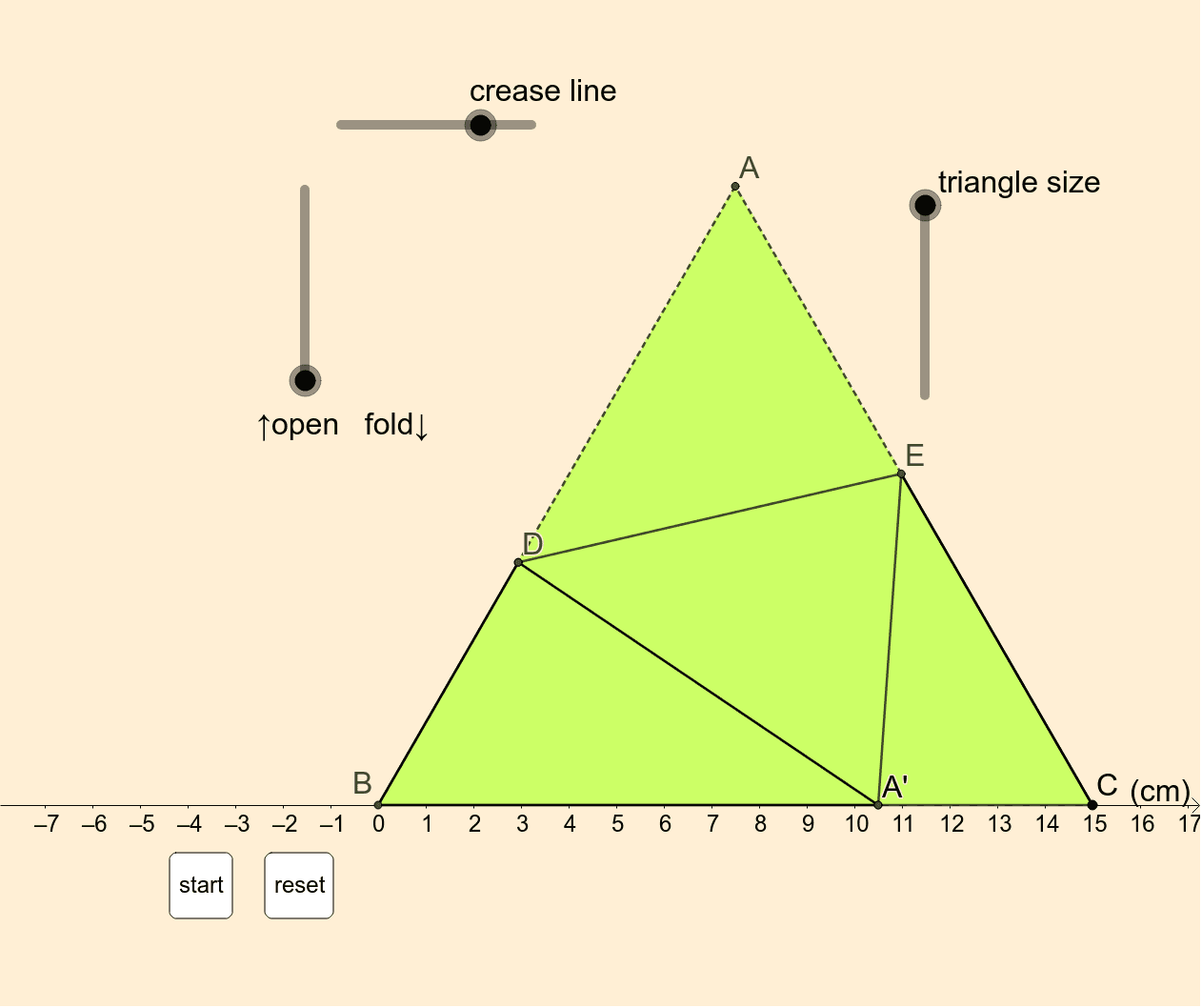



Fold Equilateral Triangle 正三角形の折り返し 相似 Geogebra




三角形の相似条件調べ Geogebra
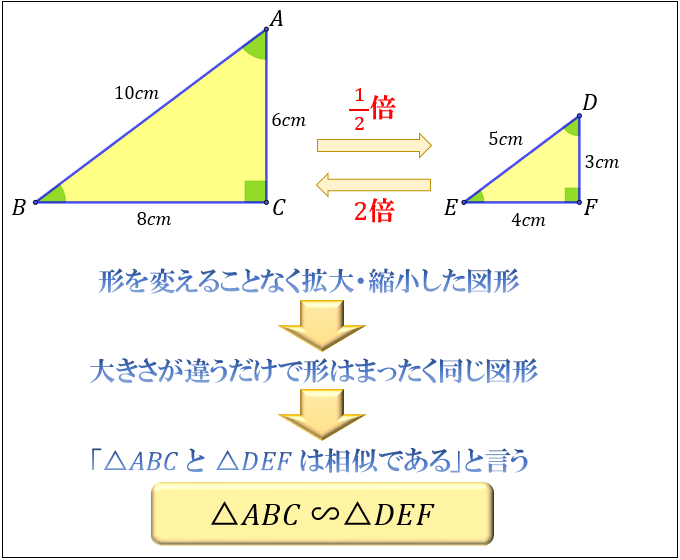



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ



1




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



相似な三角形はどれか 中学から数学だいすき
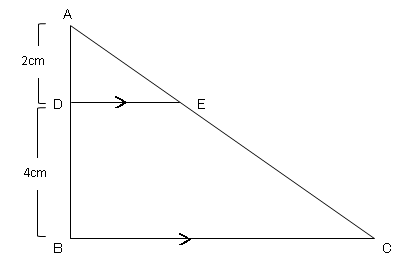



相似と面積比 1 ネット塾



三角形の 合同条件 相似条件 の意味について 三角比や正弦定理 余弦定理の理解も深くなる ここからはじめる高校数学
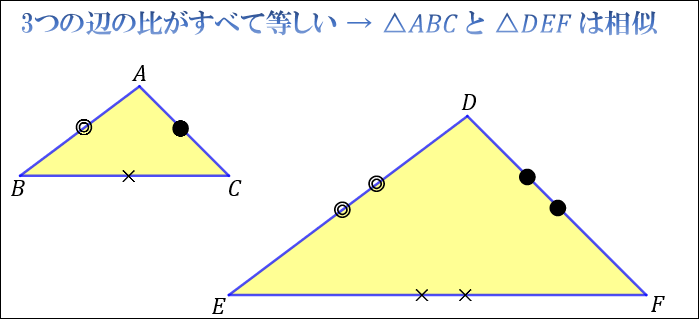



三角形の相似条件について 図解で分かる相似条件 アタリマエ



1



三角形の相似条件 修正 Youtube
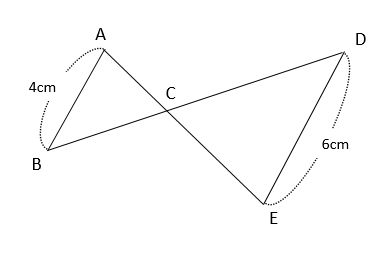



相似 平行線と三角形の問題ではちょうちょかピラミッドを探せ みみずく戦略室



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor



0 件のコメント:
コメントを投稿