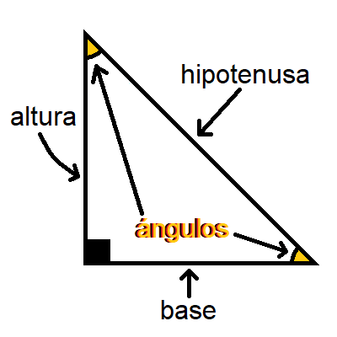
Triangulo notable 15 75 grados 151921-Triangulo notable 15 75 grados

Triángulo de 8 y grados Notable de 36 y 54 grados Triángulo de 18 y 72 grados Triangulo de 15 y 75 grados Triángulo notable de 37/2 grados Triángulo notable de 53/2 grados Razones trigonométricas Las razones trigonométricas de un ángulo agudo, se refiere a la relación que existe entre los lados de un triángulo respecto a un ánguloLos ángulos reales de este triángulo 3687 y 5313 30 y 60 grados Triángulo notable 30 y 60 (treinta y sesenta), este triángulo tiene una longitud de hipotenusa que es el doble del tamaño del triángulo del gueto 15 y 75 grados Triángulo notable 15 y 75Nuestra misión es proporcionar una educación gratuita de clase mundial para cualquier persona en cualquier lugar Khan Academy es una organización sin fines de lucro 501(c)(3)

Todo Los Triangulos Notables Sus Angulos Medidas

Triangulo notable 15 75 grados

Triangulo notable 15 75 grados-Encuentre la mejor selección de fabricantes triangulos de grados y catálogo de productos triangulos de grados baratos de alta calidad para el mercado deRazones trigonométricas de triángulos especiales Aprende a determinar el seno, coseno y tangente de triángulos y también de tríangulos Hasta ahora hemos utilizado la calculadora para evaluar el seno, coseno y tangente de un ángulo Sin embargo, es posible determinar las funciones trigonométricas de ciertos ángulos

Resolucion De Triangulos Superprof

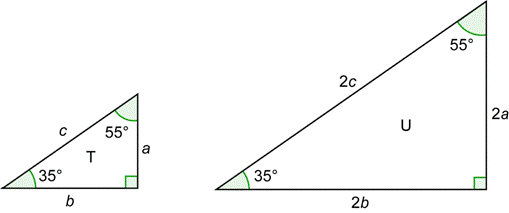
TRIGONOMETRÍA 5 RAZONES TRIGONOMÉTRICAS DE 210º 😈 Razones inversas y Angulos notables 😈 Razones trigonométricas de 0, 30, 45, 60, 90,180 270 y 360 😈 Funciones trigonometricas para 0 90 180 y 270 grados 😈 Razones trigonométricas de 45°, 60° yUn triángulo 30°60°90° es comúnmente encontrado como un triángulo rectángulo cuyos lados están en la proporción Las medidas de los lados son x , , y 2 x En un triángulo 30°60°90°, la longitud de la hipotenusa es dos veces la longitud del cateto más corto, y la longitud del cateto más largo es veces la longitud del cateto15 Paso 3 Hallar 𝑏 16 Paso 3 Hallar 𝑏El seno de un ángulo es cateto opuesto sobre hipotenusa 17 Paso 3 Hallar 𝑏El seno de un ángulo es cateto opuesto sobre hipotenusasen 65° =𝑏9,46 18 Paso 3 Hallar 𝑏Calculamos 𝑏sen 65° =𝑏9,46𝑏 = 9,46 sen 65° 19

Razones trigonométricas de 30º, 45º y 60º Regla nemotécnica para calcular los ángulos notablesGeometria, Ángulos de 45 y 135 Grados Teoremas y Problemas (Spanishlanguage version, English as a second language ESL) Educacion Matematica Tengo un carro discompuesto arriba de una colina un angulo de 75° grados del lugar donde fui a pedir ayuda con una longitud de 16 m ¡ Cual seria la distancia para pedir ayuda?

Scribd es red social de lectura y publicación más importante del mundoÁrea del Triangulo, Angulo de 30 Grados, Circunferencia Inscrita, Incentro, Tangente Problema de Geometría 618 Área del Triangulo, Angulo de 60 Grados, Circunferencia Inscrita, Incentro, Tangente Problema de Geometría 405 Cuadrilatero, 60, 75, y 135 grados, Punto Medio Problema de Geometría 368Ayudenme con esta tarea por fis 1 Ver respuesta

3

Triangulos Notables Wikipedia La Enciclopedia Libre

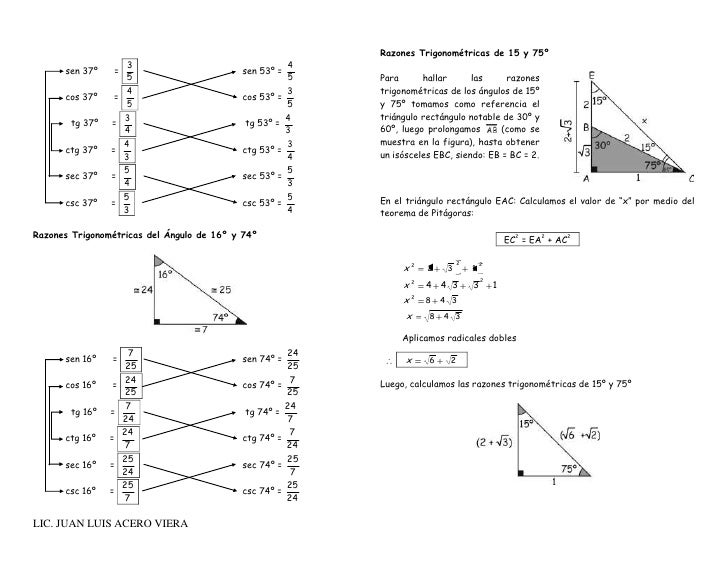
15°, 30°, 45° y 60° En base a ésta información, uno puede calcular en forma exacta, los valores de las funciones seno y coseno cada 15° Analizando el primer cuadrante, tenemos los valores exactos de 15°, 30°, 45°, 60° y 75° Hay que notar que para el ángulo de 75°, puede ser generado por la suma de 30° más 45°Simplemente introduce el ángulo deseado, en grados o radianes, y pulsa la tecla correspondiente , ó Cómo deducir razones de los ángulos de 30º y 60º Si cogemos un triángulo equilatero ABC, que como recordarás tiene todos sus lados (l) y sus ángulos iguales (60º ó π/3 rad ), y lo dividimos por la mitad obtendremos dos triángulos  Jesus Mendez Leer Teoría Triángulo Notable de 15° y 75° previous Razones trigonométricas de ángulos notables Parte II next Triángulo Notable

Triangulos Notables Ejercicios Resueltos Pdf

Todo Los Triangulos Notables Sus Angulos Medidas

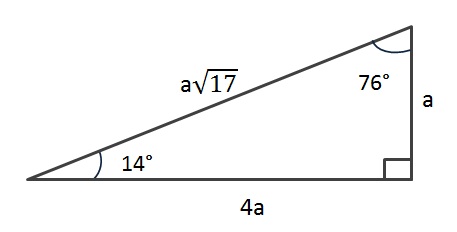
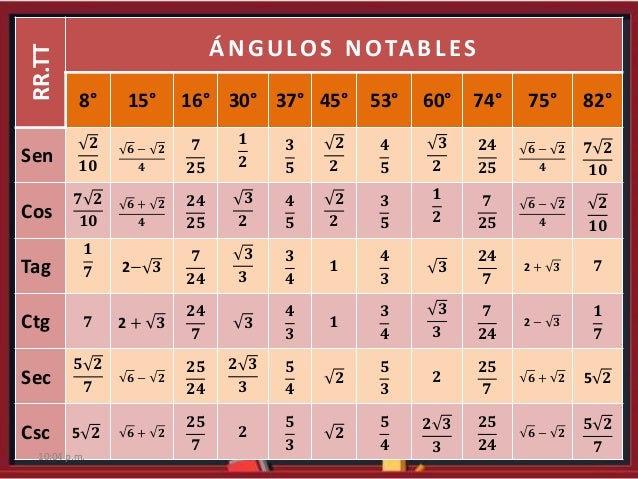
 Los más conocidos son de 45°, 37° y 53°, 60° y 30°, 15° y 75°, 74° y 16° pero los triángulos notables más usados son 45°, 37° y 53°, 60° y 30° (grados sexagesimales Elementos de un triángulo Antes de conocer los triángulos notables repasemos un poco de lo que son los elementos del triángulo En los triángulo notable existe una relación conocida entre sus lados y ángulos Los triángulos notables son de 37°, 53°, 45°, 74°,76°, 30°, 60° entre otros necesito informacion sobre el triangulo notable de º y 7º algunos trucos para memorizar cuanto es la tangente de 14 grados, pues el cociente de sus dos numeros 1/4 jeje ¡¡¡¡¡angulo que vino varias veces en examenes de admision!!!

Triangulos Rectangulos Notables Matemath Web

Triangulo Notable De 15 Y 75 6 Youtube

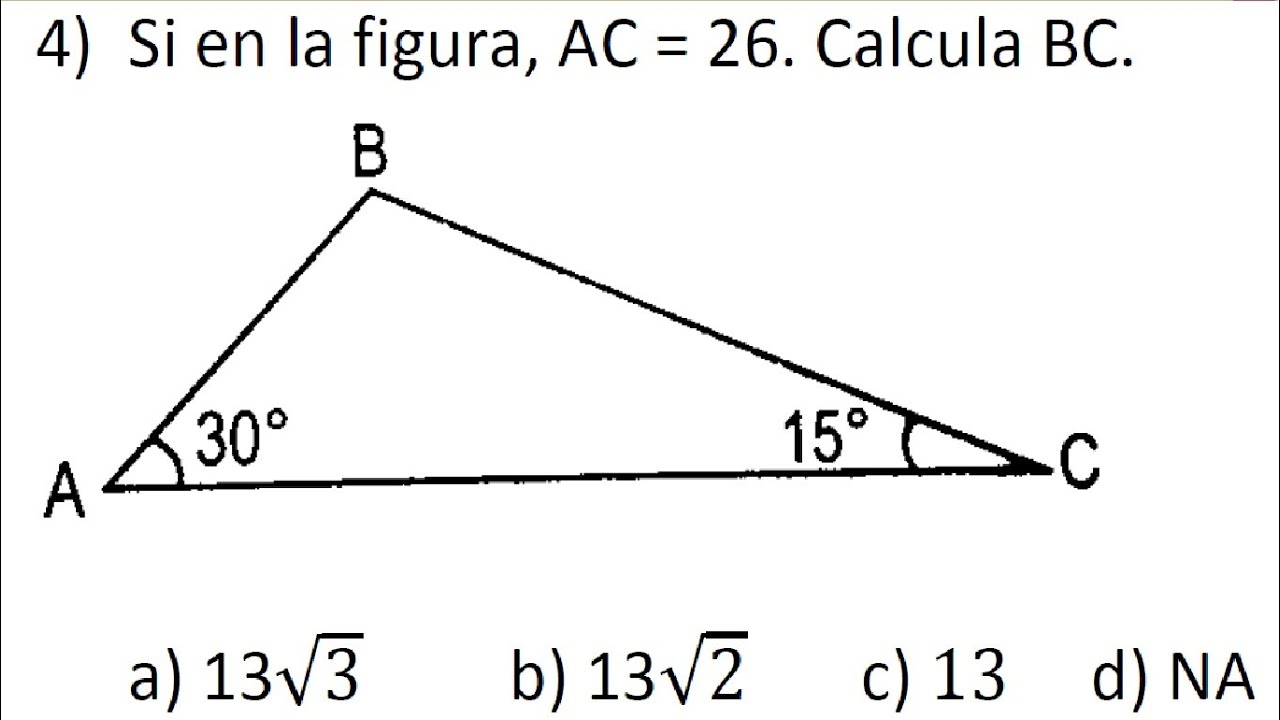
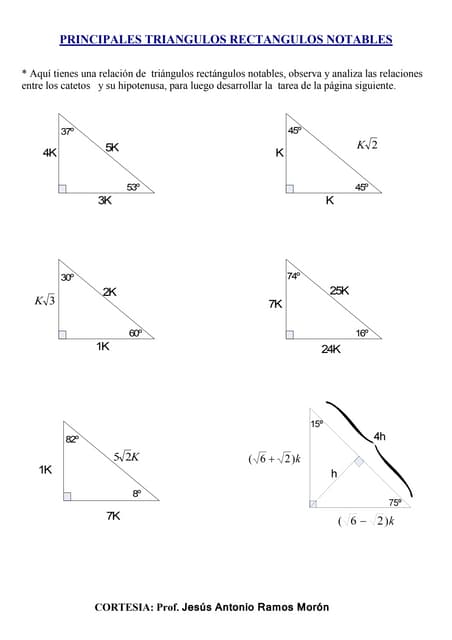
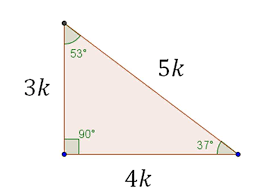
Un triángulo tiene dos ángulos que miden 35° y 75° Encontrar la medida del tercer ángulo 35° 75° x = 180° La suma de los tres ángulos interiores de un triángulo es 180° 110º x = 180º Encontrar el valor de x x = 180° ‒ 110º x = 70° Respuesta El tercer ángulo del triángulo mide 70° Ejemplo Hallar la hipotenusa del siguiente triangulo sabiendo que el ángulo que se le antepone al ángulo de 37° es 9 Explicación Triangulo Notable El cateto mas pequeño es aquel que se opone al ángulo mas pequeño y así viceversa Son aquellos triángulos que a partir de la razón About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators

Un Triangulo Rectangulo Tiene Angulos Agudos A Y B Si Y

Triangulos Notables

Un triángulo obtuso tiene un ángulo obtuso o mayor a 90 grados y dos ángulos agudos o menores a 90 grados La suma de los ángulos es igual a Ahora, es tiempo de practicar Identifica cada tipo de triángulo según sus ángulos Ejemplo A Un triángulo con ángulos que miden 60 grados recibe el nombre de _____El triángulo 45°45°90° es un triángulo rectángulo cuyos lados se encuentran comúnmente en la proporción Las medidas de los lados son x , x , y En un triángulo 45°45°90°, la longitud de la hipotenusa es por la longitud de un cateto Para ver porque es esto, dese cuenta que por el inverso del teorema de Pitágoras , estos teniendo en cuenta sus propiedades y proporciones resolveremos problemas respecto a este triangulo notable

Triangulos Rectangulos Notables Matemath Web

Triangulos Notables 15 75

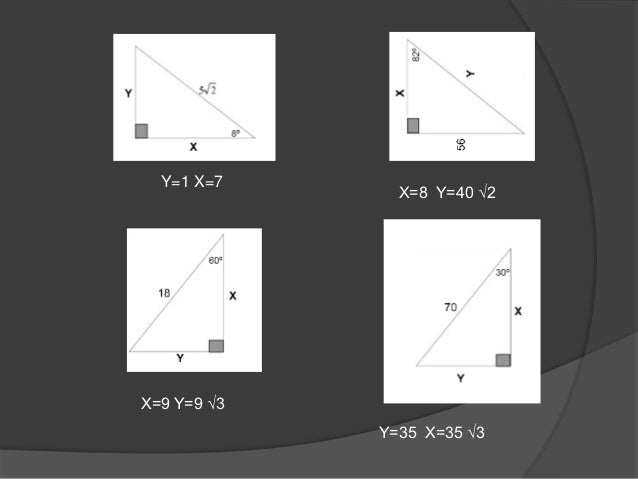
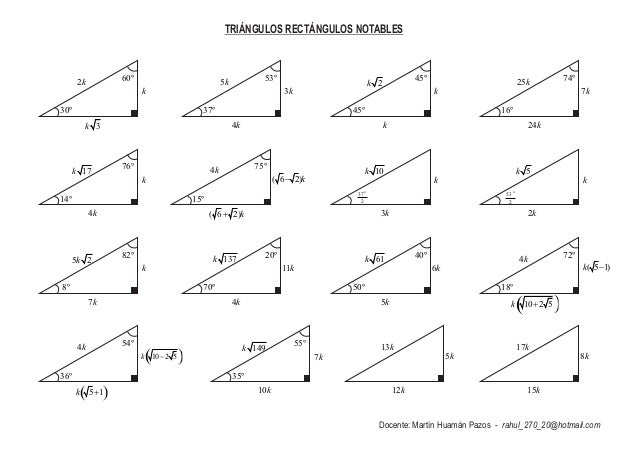
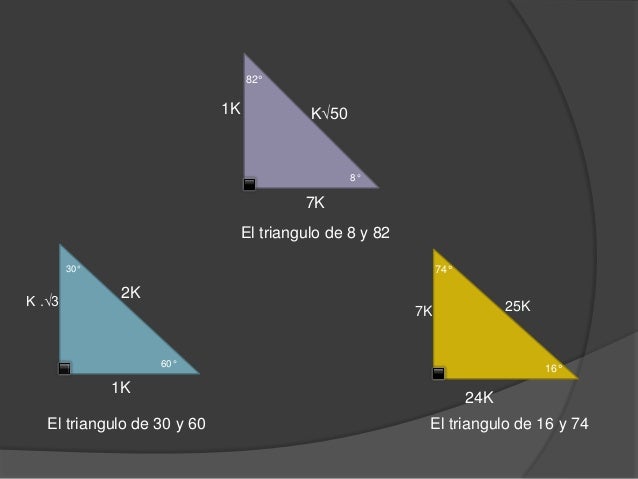
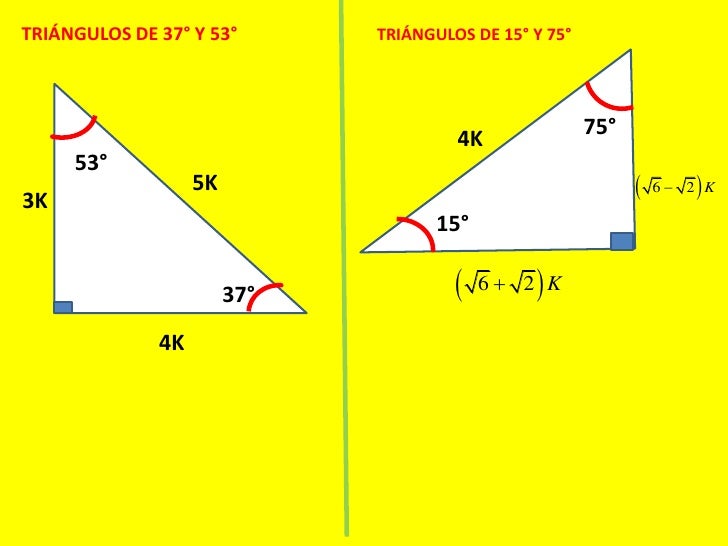
 Encuentra una respuesta a tu pregunta Triángulo notable de 23 y 67 grados 5106 5106 Matemáticas Primaria contestada Triángulo notable de 23 y 67 grados 2 Ver respuestas milyjim9 milyjim9 Respuesta Explicación paso a paso Llo también necesito la respuesta° 1K K√50 8° 7K El triangulo de 8 y 30° K √3 74° 2K 25K 7K 60° 1K El triangulo de 30 y 60 16° 24K El triangulo de 16 y 74 8 √10K K 37°/2 3K El triangulo de 37/2 75° (√6 √2)K 4K √5 K K 15° (√6 √2)K El triangulo de 15 y 75 53°/2 2K El triangulo de 53/2 9Ahora calculamos el valor de «k» y lo reemplazamos para calcular los valore de «x» e «y» A) 8 B) 16 C) 24 D) 32 E) 40 TRIANGULOS GENERICOS II objetivos Cálculo de un lado desconocido de un triángulo rectángulo conociendo un lado y un ángulo notable Se completa el ángulo que falta en el triángulo rectángulo (en este caso será 45

Aekngjyixh2wrm

Todo Los Triangulos Notables Sus Angulos Medidas

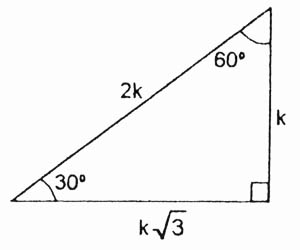
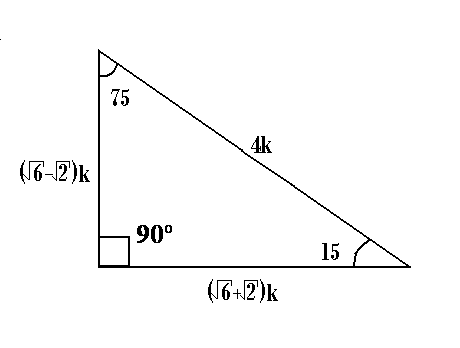
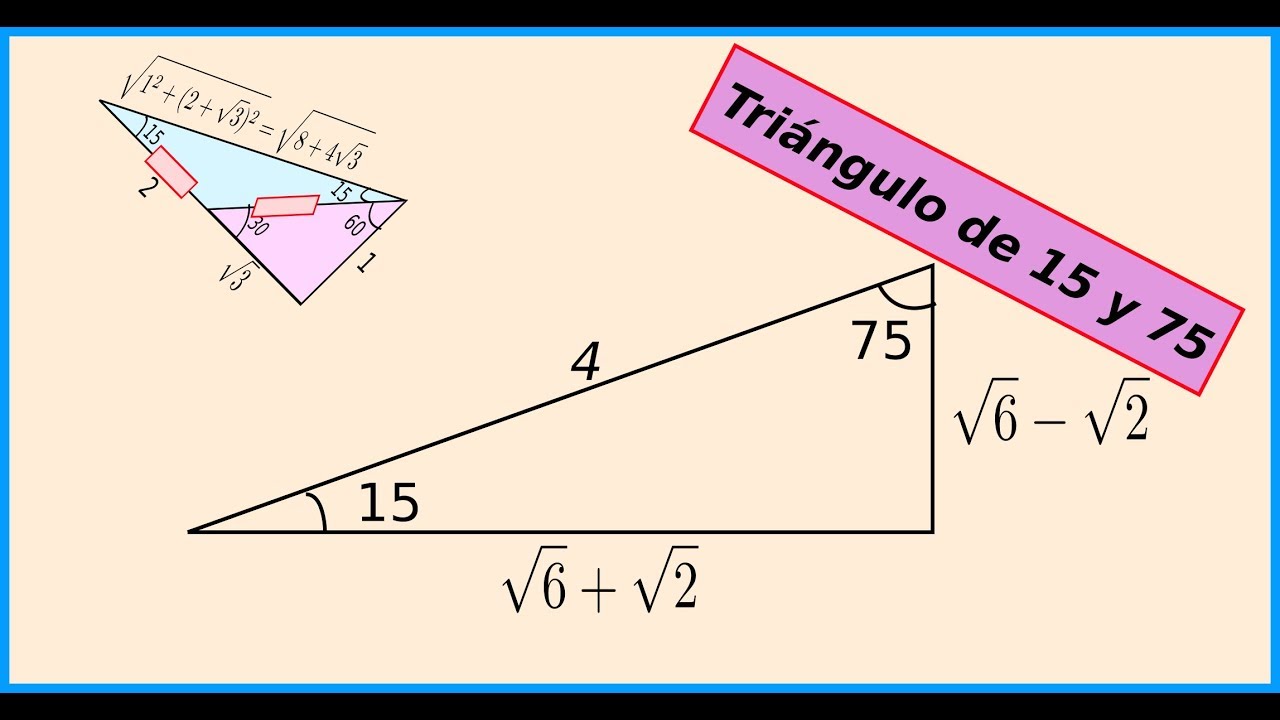
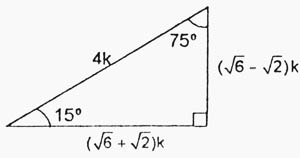
De 30 y 60 grados El triángulo notable de 30 y 60 (treinta y sesenta), este triángulo presenta una longitud de hipotenusa que es el doble del tamaño del cateto menor del triángulo De 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos De 16 y 74 gradosPortafolio matdocx PORTAFOL IO MATEM\u00c1TI CO Alumno Piero Poblete Profesora Martha Ch\u00e1vez Grado y secci\u00f3n 4to A Unidad 8 \u1cFortalecer espacios de15° 1,5 m = K( 6− 2) x = 4k 15° x 1,5 m 1,5 m = K ( 6 − 2) 1,5 m = K (2,45 –1,41) 1,44 m = k • Calculamos la longitud de la rampa cuando el ángulo es de 15° (1) representación gráfica de la rampa (2) triángulo notable de 15 y 75° Relacionamos las longitudes de los lados de ambos triángulos 1 2 En (2), calculamos el valor

Triangulo Rectangulo Notable 15 Y 75 Youtube

Es Static Z Dn Net Files D15 4da1bb799feaa7a35cfc248 Pdf

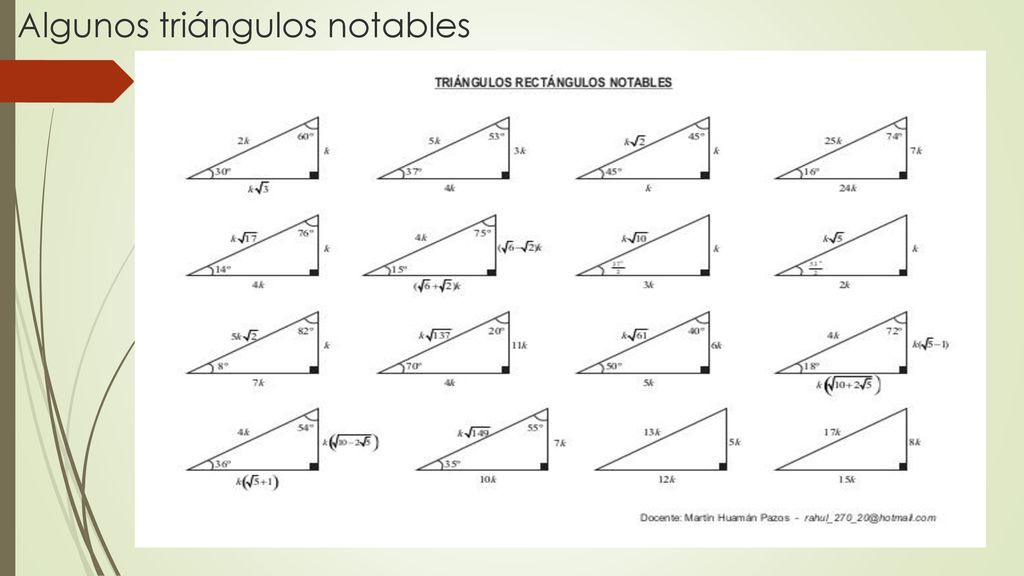
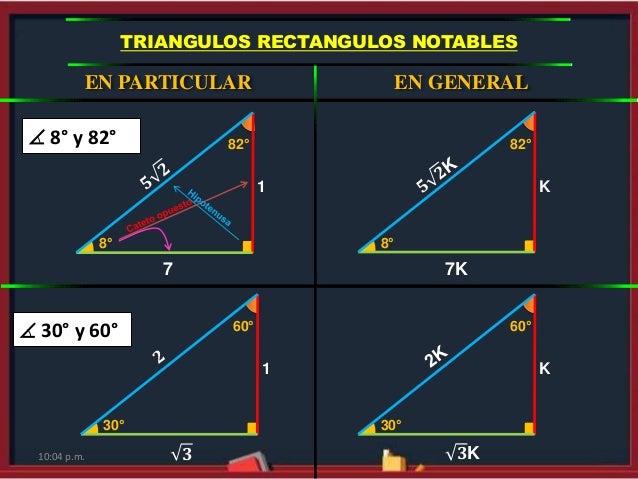
 Faltaria 70 grados para que forne el triángulo KarlaPG4 KarlaPG4 No se necesita dibujo, cualquier triángulo, los ángulos internos suman 180° entonces tienes dos ángulos 45 y 65, 45 65=110 entonces tienes que ver cuantos grados te faltan para 180°, entonces,,, =70° esa es la respuesta ) 70° Triangulos rectangulos notables (completo) 1 TRIÁNGULOS RECTÁNGULOS NOTABLES 2k k 3k 30° 60° 5k 3k 4k 37° 53° 2k k k 45° 45° 25k 7k 24k 16° 74° 17k k 4k 14° 76° 4k ( 6 2)k 15° 75° 10k k 3k 37 2 ° 5k k 2k 5 2k k 7k 8° ° 137k 11k 4k 70° ° 61k 6k 5k 50° 40° 4k ( 5 1)k ( )10 2 5k 18° 72° 4k ( )10 2 5k ( )5 1k 36 Bagg Para ambos caso el triangulo notables es el triangulo recto Debemos recordar que un triangulo recto o rectángulo es aquel que tiene un angulo de 90° Así mismo, la suma de todos los ángulos internos de un triangulo debe sumar 180° En el primer caso, tenemos los angulo 10 y 80, por lo tanto 10 80 x = 180 x = 180 90

1

Todo Los Triangulos Notables Sus Angulos Medidas

Publishing platform for digital magazines, interactive publications and online catalogs Convert documents to beautiful publications and share them worldwide Title TRIÁNGULOS NOTABLES Y POR APROXIMACIÓN, Author JUSTO GUSTAVO INGA FLORES, Length 2Triángulo notable de 16° y 74° Triángulo notable de 15° y 75° El grado de apertura de esos arcos (y no su extensión) está representado por el ángulo, sin importar cuán lejos o cerca se haga del vértice Nombres de los ángulos Según aumenta el ángulo, el nombre va cambiando La suma de los angulos interiores de todo triangulo es de 180 grados sexagesimales Entonces si te refieres a un triangulo rectángulo eso quieres decir que tiene un angulo de 90 grados, y adicionalmente mencionas que tiene un angulo agudo de 38 grados entonces 90 38 x = 180 entonces x = 52 grados Exitos

Resolucion De Triangulos Superprof

Triangulos Notables De 15

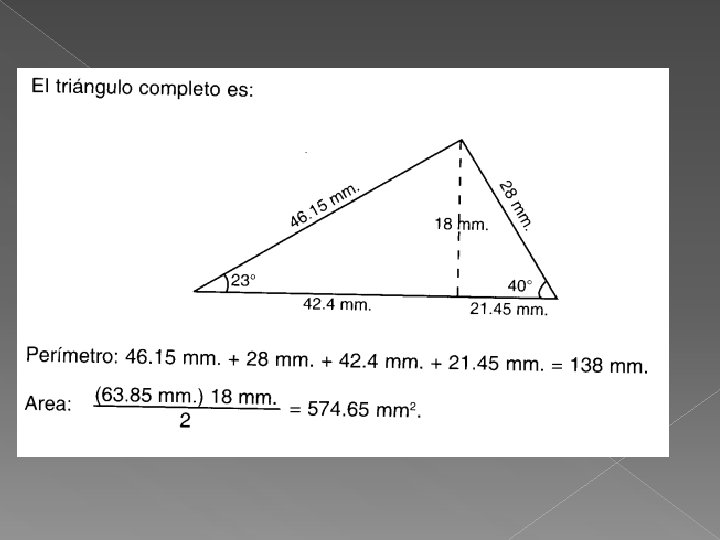
M m m 16 m 75° 16 m 43 Respuesta Incorrecta TRATA DE NUEVO 44 En los triángulo notable existe una relación conocida entre sus lados y ángulos Los triángulos notables son de 37°, 53°, 45°, 74°,76°, 30°, 60° entre otros Triangulo Triángulo Rectángulo Triángulos Notables Triángulo Notable de 15° y 75°De 30 y 60 grados El triángulo notable de 30 y 60 (treinta y sesenta), este triángulo presenta una longitud de hipotenusa que es el doble del tamaño del cateto menor del triángulo De 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos

2 Triangulos Y 3 Rectangulos Novocom Top

Resources Aprendoencasa Pe Perueduca Secundaria 5 Semana 14 Pdf S14 Sec 5 Solucion Matematica Dia 3 Pdf

Triangulos Rectangulos Notables Matemath Web

Triangulo Notable De 15 Y 75 Profesorajesus Com

Triangulos Rectangulos Notables Completo

Triangulos Notables By Nicolas Medina By Nicolasmed0123 On Emaze

Todo Los Triangulos Notables Sus Angulos Medidas

Todo Los Triangulos Notables Sus Angulos Medidas

Pdf Matematica Secundaria Piero Daniel Mescua Cossio Academia Edu

Unidad I Utilicemos Las Razones Trigonometricas Trigonometra Es

Trigonometria

Triangulos Rectangulos Notables Completo

Unidad Vii Geometria Trigonometria Y Series

Triangulo Rectangulo De 75 Y 15 Youtube

Triangulos Rectangulos Notables Matemath Web

File Triangulo Auxiliar De 75 Y 15 Png Wikimedia Commons

Triangulos Rectangulos Notables Y Pitagoricos Para Tercer Grado

Todo Los Triangulos Notables Sus Angulos Medidas

Triangulo Rectangulo Problema 7 Basico

Hallar A B Triangulos Notables Brainly Lat

Triangulos Notables De 15

Triangulos Rectangulos Notables Matemath Web

Triangulos Notable Matematica Para Secundaria

Funciones Trigonometricas De Los Angulos 15 Y 75 Youtube

Resolucion De Triangulos Superprof

Todo Los Triangulos Notables Sus Angulos Medidas

Razones Trigonometricas En El Triangulo Rectangulo Ppt Descargar

Triangulos Rectangulos Notables

Xdocs Cz Doc Triptico De Triangulos Notables Xd 6nw5057qx1n1

Resolucion De Triangulos Superprof

El Triangulo De 15 Y 75 Grados Youtube

Angulo De 15 Grados Novocom Top

Triangulo Notable De 15º Y 75º Demostracion Youtube

Todo Los Triangulos Notables Sus Angulos Medidas

Problemas De Triangulos Notables Para Tercero De Secundaria 21

Todo Los Triangulos Notables Sus Angulos Medidas

Triangulos Notables Congruencia De Triangulos Cuadrilateros Triangulo Euclides

Triangulos Rectangulos Notables Completo

Las Razones By Nanogom4 On Emaze

Razones Trigonometricas Para Cuarto De Secundaria Recursos 21

Triangulo Notable De 15º Y 75º Demostracion Youtube

Todo Los Triangulos Notables Sus Angulos Medidas

Http Www Itsmante Edu Mx Wp Content Uploads 17 11 Cuadernillo De Trigonometria Pdf

Todo Los Triangulos Notables Sus Angulos Medidas

Triangulo Rectangulo Notable De 15 Y 75 Youtube

Triangulos Notables Ejercicios Resueltos Pdf

Triangulos Notables De 15

Triangulos Notables Ejercicios Resueltos Pdf

Triangulos Notables Ejercicios Resueltos Pdf

1

Triangulos Rectangulos Notables Matemath Web

Triangulos Notables Ejercicios Resueltos Pdf

1

Sesion De Triangulos Notables Pedagogia Conceptos Psicologicos

Triangulos Notables

Triangulos Notables De 15

Triangulos Notables

Http Www Itsmante Edu Mx Wp Content Uploads 17 11 Cuadernillo De Trigonometria Pdf

Calameo Triangulos Notables Y Por Aproximacion

Calameo Angulos Notables Tabla

Capitulo 2 Triangulos By Sagradocorazon Issuu

Todo Los Triangulos Notables Sus Angulos Medidas

Todo Los Triangulos Notables Sus Angulos Medidas

Triangulos De 30 Y 60 45 Y 45 37 Y 53 Razones Trigonometricas Notables Ejercicios Res Razones Trigonometricas Ejercicios Resueltos Formulas Matematicas

Los Triangulos Rectangulos Notables Y Sus Respectivos Angulos

Triangulos Rectangulos Notables Y Pitagoricos Para Tercer Grado

Triangulos Notables By Nicolas Medina By Nicolasmed0123 On Emaze

Http Www Itsmante Edu Mx Wp Content Uploads 17 11 Cuadernillo De Trigonometria Pdf

Http Www Itsmante Edu Mx Wp Content Uploads 17 11 Cuadernillo De Trigonometria Pdf

2 Triangulos Y 3 Rectangulos Novocom Top

Triptico De Triangulos Notables Xd Triangulo Pitagoras

Triangulos Rectangulos Notables Completo

Aprendizaje Por Descubrimiento En Sistemas De Puntos Y Rectas Notables Del Triangulo

Los Triangulos Rectangulos Notables Y Sus Respectivos Angulos

Triangulos Notables By Nicolas Medina By Nicolasmed0123 On Emaze

Ejercicios Con Triangulos Oblicuangulos Superprof

Trigonometria 1ra Parte

Triangulos Rectangulos Notables

Triangulos Notables 15 75

Triangulos Notables Ejercicios Resueltos Pdf

Todo Los Triangulos Notables Sus Angulos Medidas

Unidad I Utilicemos Las Razones Trigonometricas Ppt Descargar

Triangulos Notables Ejercicios Resueltos Pdf

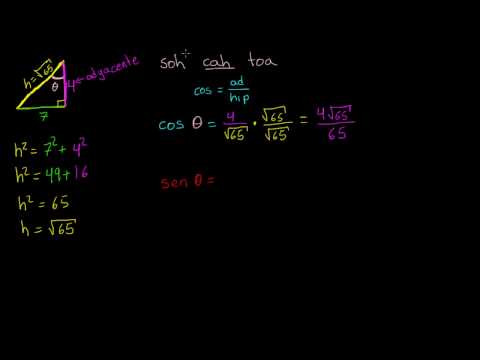
Razones Trigonometricas En Triangulos Rectangulos Video Khan Academy

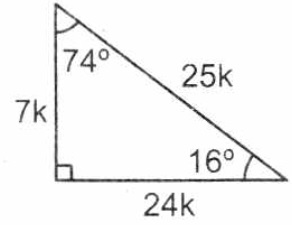
Triangulos Notables By Nicolas Medina By Nicolasmed0123 On Emaze

Triangulos Rectangulos Notables Matemath Web

Incoming Term: triangulo notable 15 75 grados, triángulo notable de 15 y 75 grados, triangulo rectangulo notable de 15 y 75 grados,